Um dos maiores motivos pelo qual qualquer metodologia de gerenciamento de projetos existe, é trazer redução de custos.
O atraso de uma semana em um projeto, gera dois custos diferentes:
- O primeiro custo é o custo das pessoas presentes no time do projeto, por terem que trabalhar por mais uma semana.
- Já o segundo, trata-se do custo de atraso (normalmente chamado de cost of delay) que por sua vez é a receita que deixa-se de receber pelo atraso, por exemplo: supondo que um novo produto tenha uma receita diária de 100 reais, o custo de atraso seria de 700 reais (100 reais x 7 dias), aqui no blog temos um post muito interessante sobre o assunto.
Como esses custos podem ser altos, é preciso utilizar ferramentas que possam dar visibilidade para as datas de entrega. Uma das formas encontradas para dar visibilidade a estes potenciais problemas, foi através da adoção do Diagrama de Gantt, para gerenciamento de projetos, nele é possível identificar os pontos mais delicados do projeto (os caminhos críticos) em que deve-se dar maior esforço para que não atrasem, visto que ao atrasar nesses pontos o projeto inteiro também irá atrasar.
Embora essa ferramenta seja ótima para alguns tipos de projetos (normalmente onde existe um grau de incerteza baixo), ela não é a ideal para projetos com previsibilidade baixa devido a variância de entregas, como ocorre em projetos que lidam com o campo do conhecimento (redigir um livro ou desenvolver software, como exemplos).
Aqui na Plataformatec temos sempre feito o máximo para que todas as nossas previsões de entregas sejam embasadas em dados e sigam métodos científicos comprovados. Os dois métodos que mais utilizamos são:
- Progressão linear
- Simulação de Monte Carlo
PROGRESSÃO LINEAR
Na progressão linear, fazemos uma análise dos dados de itens de trabalho entregues durante algum período (normalmente trabalhamos com periodicidade semanal) e através de uma análise destes valores elegemos quais são os melhores valores a serem alocados na progressão. Por exemplo: supondo que tenhamos os valores de histórico de itens de trabalho entregues por semana (throughput), conforme o gráfico abaixo:
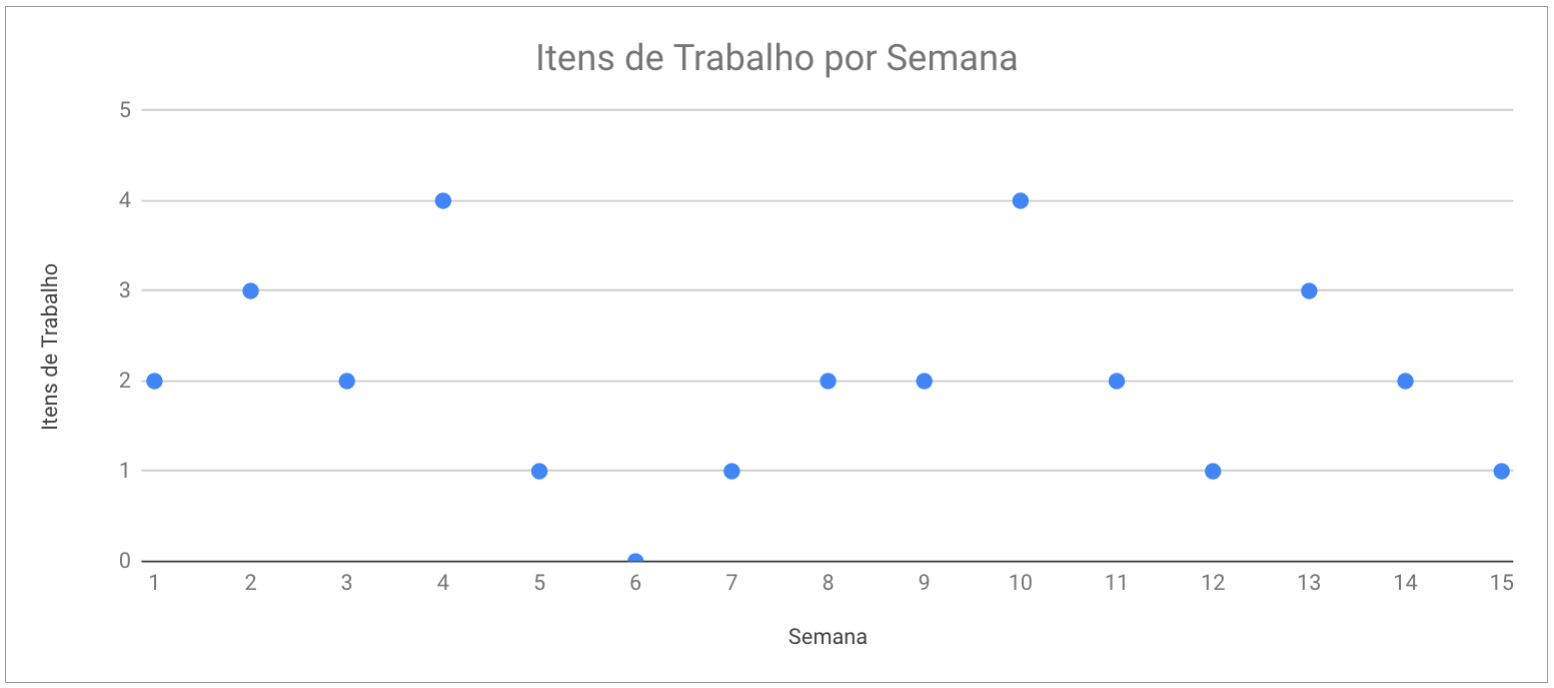
Um valor que faz sentido para a progressão pessimista será de que a cada semana iremos entregar 1 item de trabalho por semana, visto que tivemos 5 casos em que a entrega foi de 1 ou 0, para a estimativa otimista podemos utilizar o valor 3 ou 4 ou até mesmo 3,5 visto que tivemos 4 casos em que o valor foi 3 ou mais, por fim para a progressão provável o melhor valor seria o de 2 visto que é o valor da mediana do dataset e é o valor que mais aparece (a moda).
O maior problema da progressão linear é de que estamos informando os valores a serem utilizados para cada cenário, algo que pode ser perigoso caso a pessoa que está fazendo a progressão não tenha um bom domínio de análise de dados. Além disso, a progressão linear também ignora a variância. Desta forma, em sistemas com uma variância de entrega muito elevada, a progressão linear pode não fazer tanto sentido.
MONTE CARLO
Outra técnica que utilizamos chama-se Monte Carlo, para entender melhor como o método funciona, bem como ter uma inferência do que ele faz, recomendo esse blogpost que é bem completo.
Tenho utilizado o método desde que entrei na Plataformatec com grande sucesso, porém uma coisa sempre ficava na minha mente era: “Quantas iterações são necessárias para que eu possa ter um bom grau de confiabilidade no método?”. Para responder essa pergunta eu fiz muitas pesquisas em livros estatísticos e pela internet e não consegui encontrar nenhum tipo de informação que me auxiliasse.
Dessa forma resolvi fazer um estudo desse assunto. O objetivo do Monte Carlo é de inferir a probabilidade de algum evento, “forçando” que o evento ocorra tantas vezes que o resultado me dê a probabilidade da ocorrência do evento. Por exemplo, ao lançar uma moeda mil vezes se eu contar quantas vezes a moeda cai em “cara” e dividir esse valor pelas mil vezes que a moeda foi lançada, obterei uma inferência da probabilidade da moeda cair em “cara”.
Para conseguir saber a qualidade do método eu realizei testes nos quais eu já sabia o resultado esperado, e fui fazendo com que o problema fosse cada vez mais complexo, de forma a ver se existe alguma relação entre a dificuldade do problema e a quantidade de iterações necessárias para que o valor inferido pelo método seja o mais próximo possível do valor calculado.
O objetivo é verificar quantas iterações são necessárias para que o erro entre o valor inferido pelo método e o valor calculado seja mínimo (para previsões de probabilidade de entrega um erro a partir da segunda ou terceira casa decimal é bem aceitável). Gostaria de ressaltar que esse blogpost não é um estudo científico acerca do assunto, e seu objetivo é entender através de inferência qual é um valor de iterações bom para ser utilizado em predições para projetos.
OS TESTES
Os testes foram todos realizado utilizando a linguagem de programação R, que pode ser baixado neste link. Caso prefira utilizar um IDE, recomendo o RStudio.
Em todos os testes eu rodei o sistema por 100 vezes utilizando as seguintes quantidades de iterações: 100 (cem), 1000 (mil), 10000 (dez mil), 100000 (cem mil), 1000000 (um milhão), 10000000 (dez milhões), 100000000 (cem milhões) e 200000000 (duzentos milhões). Os resultados são os consolidados dessas 100 “rodadas”, em cada iteração.
A MOEDA
O primeiro teste que fiz foi em cima de um lançamento de moeda. Uma moeda tem 50% de chance de cair em qualquer um de seus lados e este é o valor que queremos que seja inferido pelo Monte Carlo. Para isso utilizei o seguinte código em R:
LancaMoeda <- function(iteracoes)
{
# Cria o vetor com os valores possíveis para a moeda 1 = Cara e 0 = Coroa
moeda = c(0,1)
resultado = 0
# Soma todos os resultados em que a moeda foi "Cara"
resultado = sum(sample(moeda, iteracoes, replace=T))
# Divide o valor pela quantidade de iterações e transforma em percentual
resultado = (resultado/iteracoes) * 100
return(resultado)
}
# Inicializa variáveis
vetor_resultado = 0
vetor_tempo = 0
controle = 0
# Informa a quantidade de iterações a serão executadas
rodadas = 100
# Aloca os resultados percentuais em um vetor de 100 itens e aloca os tempos de execução em outro
while (controle != 100)
{
tempo_inicial = Sys.time()
vetor_resultado = append(vetor_resultado, LancaMoeda(rodadas))
tempo_final = Sys.time()
tempo = tempo_final - tempo_inicial
vetor_tempo = append(vetor_tempo, tempo)
controle = controle + 1
}
# Mostra os percentuais
vetor_resultado
# Mostra os tempos de execução
vetor_tempo
Alterando os valores da variável iterações e compilando os resultados obtive a seguinte tabela:
| Iterações | Resultado Min | Resultado Max | Resultado Esperado | Resultado Médio | Resultado Médio - Resultado Esperado | Mediana do Resultado | Mediana Resultado - Resultado Esperado | Desvio-Padrão do Resultado |
|---|---|---|---|---|---|---|---|---|
| 100 | 33.00000 | 67.00000 | 50.00000 | 50.02000 | 0.02000 | 50.00000 | 0.00000 | 5.09368 |
| 1000 | 43.60000 | 56.20000 | 50.00000 | 49.99440 | 0.00560 | 50.00000 | 0.00000 | 1.59105 |
| 10000 | 48.35000 | 51.78000 | 50.00000 | 50.01263 | 0.01263 | 50.02000 | 0.02000 | 0.51001 |
| 100000 | 49.58000 | 51.78000 | 50.00000 | 49.99110 | 0.00890 | 49.99350 | 0.00650 | 0.15805 |
| 1000000 | 49.85170 | 50.15090 | 50.00000 | 49.99883 | 0.00117 | 49.99785 | 0.00215 | 0.04811 |
| 10000000 | 49.95433 | 50.05807 | 50.00000 | 50.00013 | 0.00013 | 50.00010 | 0.00010 | 0.01564 |
| 100000000 | 49.98435 | 50.01637 | 50.00000 | 50.00004 | 0.00004 | 49.99989 | 0.00011 | 0.00516 |
| 200000000 | 49.98890 | 50.01195 | 50.00000 | 49.99981 | 0.00019 | 49.99987 | 0.00013 | 0.00345 |
No caso de um problema simples, como o lançamento de uma moeda, podemos ver que a quantidade ideal de iterações seria algo entre 10 e 100 milhões de vezes. Visto que é nessa faixa em que o desvio padrão dos resultados começa a ser na ordem da terceira casa decimal, outro ponto interessante é que se você deseja mostrar apenas a primeira casa decimal um valor de 1 milhão de iterações já atenderia.
O DADO
Com o teste da moeda podemos ter uma idéia de quantas iterações são necessárias, para cada grau de confiabilidade desejado. Porém uma pergunta que fica é se esse comportamento é o mesmo para sistemas mais complexos. Por este motivo fiz um teste parecido, porém agora rodando um dado de 6 lados, que tem 16,67% de chances de cair em qualquer face.
RolaDado <- function(iteracoes)
{
# Cria o vetor com os valores possíveis para o dado
dado = 1:6
resultado = 0
# Aloca os resultados das rolagens do dado
resultado = sample(dado,iteracoes,replace=T)
# Soma todos os valores que tiverem sigo iguais a 6
resultado = sum(resultado == 6)
# Divide o valor pela quantidade de iterações e transforma em percentual
resultado = (resultado/iteracoes) * 100
return(resultado)
}
# Inicializa variáveis
vetor_resultado = 0
vetor_tempo = 0
controle = 0
# Informa a quantidade de iterações a serão executadas
rodadas = 100
# Aloca os resultados percentuais em um vetor de 100 itens e aloca os tempos de execução em outro
while(controle != 100)
{
tempo_inicial = Sys.time()
vetor_resultado = append(vetor_resultado, RolaDado(rodadas))
tempo_final = Sys.time()
tempo = tempo_final - tempo_inicial
vetor_tempo = append(vetor_tempo, tempo)
controle = controle + 1
}
# Mostra os percentuais
vetor_resultado
# Mostra os tempos de execução
vetor_tempo
Alterando os valores da variável iterações e compilando os resultados obtive a seguinte tabela:
| Iterações | Resultado Min | Resultado Max | Resultado Esperado | Resultado Médio | Resultado Médio - Resultado Esperado | Mediana do Resultado | Mediana Resultado - Resultado Esperado | Desvio-Padrão do Resultado |
|---|---|---|---|---|---|---|---|---|
| 100 | 6.00000 | 28.00000 | 16.66667 | 16.58100 | -0.08567 | 16.00000 | -0.66667 | 3.64372 |
| 1000 | 13.20000 | 20.40000 | 16.66667 | 16.68500 | 0.01833 | 16.60000 | -0.06667 | 1.16949 |
| 10000 | 15.60000 | 17.94000 | 16.66667 | 16.65962 | -0.00705 | 16.67000 | 0.00333 | 0.38072 |
| 100000 | 16.22200 | 17.06200 | 16.66667 | 16.66109 | -0.00557 | 16.66500 | -0.00167 | 0.11356 |
| 1000000 | 16.54960 | 16.54960 | 16.66667 | 16.66616 | -0.00050 | 16.66790 | 0.00123 | 0.03650 |
| 10000000 | 16.63294 | 16.70266 | 16.66667 | 16.66607 | -0.00060 | 16.66577 | -0.00090 | 0.01220 |
| 100000000 | 16.65592 | 16.67948 | 16.66667 | 16.66670 | 0.00004 | 16.66679 | 0.00012 | 0.00372 |
| 200000000 | 16.65787 | 16.67476 | 16.66667 | 16.66671 | 0.00004 | 16.66671 | 0.00004 | 0.00267 |
Podemos ver que neste caso também temos que a quantidade ideal de iterações seria algo entre 10 e 100 milhões de vezes, para termos um erro a partir da segunda ou terceira casa decimal. Esse resultado mostra que, ou a complexidade do problema não tem influência na quantidade de iterações ou de que o problema da moeda e do dado têm complexidades parecidas. Analisando os tempos de execuções da moeda e do dado verifica-se que eles demoram tempos parecidos de execução, o que corrobora a hipótese de que os problemas tem complexidades próximas.
DOIS DADOS
Para saber se a complexidade era muito próxima e por isso que os valores de iterações ideais ficaram iguais, decidi dobrar a complexidade do problema ao rodar dois dados em vez de um (entendo que nem sempre ao dobrar a quantidade de funções teremos mais complexidade por conta da ordem de complexidade ou Big-O Notation, porém fiz o teste para ter certeza se isso se aplicava). A maior probabilidade de resultado encontrada ao rolar dois dados é o valor 7, tendo 16,67% de chances de ocorrer.
RolaDoisDados <- function(iteracoes)
{
# Cria o vetor com os valores possíveis para o dado
dado = 1:6
resultado = 0
# Aloca os resultados das rolagens dos dados
primeira_rolagem = sample(dado,iteracoes,replace=T)
segunda_rolagem = sample(dado,iteracoes,replace=T)
# Soma os vetores, item a item
resultado = primeira_rolagem + segunda_rolagem
# Soma todos os valores que tiverem sigo iguais a 7
resultado = sum(resultado == 7)
# Divide o valor pela quantidade de iterações e transforma em percentual
resultado = (resultado/iteracoes) * 100
return(resultado)
}
# Inicializa variáveis
vetor_resultado = 0
vetor_tempo = 0
controle = 0
# Informa a quantidade de iterações a serão executadas
rodadas = 100
# Aloca os resultados percentuais em um vetor de 100 itens e aloca os tempos de execução em outro
while(controle != 100)
{
tempo_inicial = Sys.time()
vetor_resultado = append(vetor_resultado, RolaDoisDados(rodadas))
tempo_final = Sys.time()
tempo = tempo_final - tempo_inicial
vetor_tempo = append(vetor_tempo, tempo)
controle = controle + 1
}
# Mostra os percentuais
vetor_resultado
# Mostra os tempos de execução
vetor_tempo
Novamente alterando os valores da variável iterações e compilando os resultados:
| Iterações | Resultado Min | Resultado Max | Resultado Esperado | Resultado Médio | Resultado Médio - Resultado Esperado | Mediana do Resultado | Mediana Resultado - Resultado Esperado | Desvio-Padrão do Resultado |
|---|---|---|---|---|---|---|---|---|
| 100 | 5.00000 | 31.00000 | 16.66667 | 16.37100 | -0.29567 | 16.00000 | -0.66667 | 3.77487 |
| 1000 | 13.40000 | 21.80000 | 16.66667 | 16.64710 | -0.01957 | 16.60000 | -0.06667 | 1.18550 |
| 10000 | 15.33000 | 17.77000 | 16.66667 | 16.68307 | 0.01640 | 16.68500 | 0.01833 | 0.38059 |
| 100000 | 16.23100 | 17.06600 | 16.66667 | 16.66546 | -0.00120 | 16.66800 | 0.00133 | 0.11597 |
| 1000000 | 16.54450 | 16.81170 | 16.66667 | 16.66657 | -0.00010 | 16.66860 | 0.00193 | 0.03798 |
| 10000000 | 16.62888 | 16.70282 | 16.66667 | 16.66683 | 0.00016 | 16.66705 | 0.00038 | 0.01155 |
| 100000000 | 16.65408 | 16.67899 | 16.66667 | 16.66669 | 0.00002 | 16.66673 | 0.00007 | 0.00382 |
| 200000000 | 16.65881 | 16.67455 | 16.66667 | 16.66675 | 0.00009 | 16.66682 | 0.00015 | 0.00258 |
Novamente verificamos que uma quantidade de iterações entre 10 e 100 milhões traz uma variação baixa o suficiente para ser confiável. E nesse caso pude identificar que o problema era sim mais complexo, visto que o tempo de execução para 200 milhões de vezes levou em média 7,47 segundos a mais que o problema de um único dado.
CINCO DADOS
A inferência que tive até este momento é de que a complexidade do problema influi muito pouco na quantidade de iterações a serem realizadas, mas para ter certeza eu fiz o teste com 5 dados. A maior probabilidade de resultado encontrada ao rolar cinco dados são os valores 17 e 18, tendo 10,03% de chances de ocorrer.
RolaCincoDados <- function(iteracoes)
{
# Cria o vetor com os valores possíveis para o dado
dado = 1:6
resultado = 0
# Aloca os resultados das rolagens dos dados
primeira_rolagem = sample(dado,iteracoes,replace=T)
segunda_rolagem = sample(dado,iteracoes,replace=T)
terceira_rolagem = sample(dado,iteracoes,replace=T)
quarta_rolagem = sample(dado,iteracoes,replace=T)
quinta_rolagem = sample(dado,iteracoes,replace=T)
# Soma os vetores, item a item
resultado = primeira_rolagem + segunda_rolagem + terceira_rolagem + quarta_rolagem + quinta_rolagem
# Soma todos os valores que tiverem sigo iguais a 18
resultado = sum(resultado == 18)
# Divide o valor pela quantidade de iterações e transforma em percentual
resultado = (resultado/iteracoes) * 100
return(resultado)
}
# Inicializa variáveis
vetor_resultado = 0
vetor_tempo = 0
controle = 0
# Informa a quantidade de iterações a serão executadas
rodadas = 10
# Aloca os resultados percentuais em um vetor de 100 itens e aloca os tempos de execução em outro
while(controle != 100)
{
tempo_inicial = Sys.time()
vetor_resultado = append(vetor_resultado, RolaCincoDados(rodadas))
tempo_final = Sys.time()
tempo = tempo_final - tempo_inicial
vetor_tempo = append(vetor_tempo, tempo)
controle = controle + 1
}
# Mostra os percentuais
vetor_resultado
# Mostra os tempos de execução
vetor_tempo
Compilando os resultados:
| Iterações | Resultado Min | Resultado Max | Resultado Esperado | Resultado Médio | Resultado Médio - Resultado Esperado | Mediana do Resultado | Mediana Resultado - Resultado Esperado | Desvio-Padrão do Resultado |
|---|---|---|---|---|---|---|---|---|
| 100 | 2.00000 | 20.00000 | 10.03086 | 10.04300 | 0.01214 | 10.00000 | -0.03086 | 3.01268 |
| 1000 | 6.80000 | 13.40000 | 10.03086 | 10.04160 | 0.01074 | 10.00000 | -0.03086 | 0.96373 |
| 10000 | 9.07000 | 11.03000 | 10.03086 | 10.04600 | 0.01514 | 10.04500 | 0.01414 | 0.30501 |
| 100000 | 9.74700 | 10.31500 | 10.03086 | 10.02726 | -0.00360 | 10.03100 | 0.00014 | 0.09366 |
| 1000000 | 9.95030 | 10.11240 | 10.03086 | 10.02994 | -0.00092 | 10.03045 | -0.00041 | 0.02945 |
| 10000000 | 10.00060 | 10.06768 | 10.03086 | 10.03072 | -0.00014 | 10.03065 | -0.00022 | 0.00956 |
| 100000000 | 10.02151 | 10.04116 | 10.03086 | 10.03091 | 0.00004 | 10.03102 | 0.00016 | 0.00310 |
E mais uma vez podemos ver que entre 10 e 100 milhões é valor ideal. Interessante notar que esse caso realmente foi mais complexo, levando 35 segundos a mais em média quando comparada com a rolagem de um único dado.
Conclusão
Depois de realizar todos esses testes, é possível concluir que, para a utilização em gerenciamento de projetos, uma quantidade de iterações entre 10 e 100 milhões atenderia adequadamente a necessidade de prever alguma data de entrega.
O valor que tenho utilizado é de 10 milhões, quando vou passar os dados para algum stakeholder. Porém como o processo fica demorado (em média de 30 minutos para rodar com 10 milhões), quando eu preciso verificar os dados no dia-a-dia utilizo algum valor menor (algo entre 100 mil a 1 milhão).
E você? Tem utilizado o método? Se sim, quais valores de iterações têm usado para a análise? Os resultados obtidos tem tido valor para os stakeholders de seus projetos? Caso queira trocar experiências, podemos iniciar um bate-papo por e-mail, através do endereço gabriel.lopes@plataformatec.com.br